前提准备
在开始质数的讨论之前,我们先预备一下:
质数的定义:若一个正整数除了1和它自身之外不能被任何自然数整除,则该数称为质数,也叫素数。否则为合数 。
由定义可知,所有 小于等于1的数既不是质数,也不是合数 。
质数的分布较为稀疏,对于一个足够大的数S,不超过S的质数大约有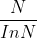 个,也就是说每InN个数约有一个质数,
这点读者了解即可。
个,也就是说每InN个数约有一个质数,
这点读者了解即可。
质数的判断(试除法)
对于质数的判断,最简单也最容易想到的方法就是一个一个的筛选,也叫试除法。
如果要判断一个数N,那么我们要对2~N-1的所有数都筛选一遍吗,显然不用。首先肯定的是N-1肯定不能整除N,那么是否能进一步缩小范围。我先给出答案:2~sqrt(N)
严谨的证明过程如下图:(注释: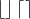 分别表示向下,向上取整)
分别表示向下,向上取整)

那好,利用这个性质,我们就可以写出一下代码:
Code(O(sqrt(N)))
尽管如此,这个代码还是优化了许多,我们单独考虑2这个情况,然后从3开始只枚举奇数。
难道这就是最快的算法吗?
Miller-Robbin算法
其实还有一个更厉害的算法,名为Miller-Robbin算法,要想学会,我们首先需要理解一个定理:
费马小定理:
对于一个质数 p,任意一个自然数a,那么: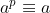 (mod p)
(mod p)
证明如下图所示:
