图像的几何变换主要包括:平移、旋转、缩放、剪切、仿射、透视等。
图像的几何变换主要分为:刚性变换、相似变换、仿射变换和透视变换(也称为投影变换)。
刚性变换:平移、旋转;
相似变换:缩放、剪切;
仿射变换:从一个二维坐标系变换到另一个二维坐标系的过程,属于线性变换。通过已知3对坐标点便可求取变换矩阵。
透视变换:从二维坐标系变换到三维坐标系,在从三维坐标系投影到二维平面,属于非线性变换。通过已知4对坐标点便可求取变换矩阵。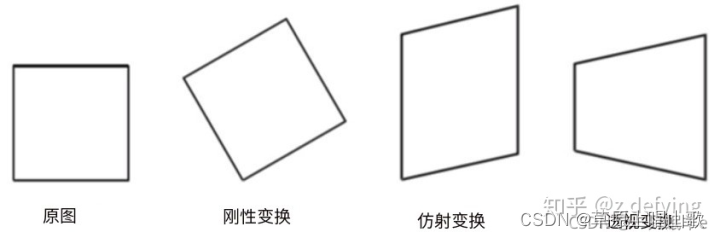
仿射变换
仿射变换是把一个二维坐标系转换到另一个二维坐标系的过程,在转换过程中坐标点的相对位置和属性不发生变换,属于线性变换。在该变换过程中只发生平移和旋转,因此一个菱形在发生仿射变换后还是一个菱形。
也可以说,仿射变换是指在向量空间中进行一次线性变换(乘以线性矩阵)和一次平移(加上一个向量),变换到另一个向量空间的过程。
仿射变换代表的是两幅图像之间的映射关系,仿射变换矩阵为2X3的矩阵,
总的来说,仿射=平移+旋转。
仿射变换Python例子
效果图
原图
透视变换后的效果图
透视变换
透视变换是将一个图像投影到新的视平面,该过程包括:1.将二维坐标系转换为三维坐标系;2.将三维坐标系投影到新的二维坐标系。该过程属于非线性变换过程,一个菱形在经过非线性变换后得到一个四边形,但是不在平行。
透视变换又可以称为投影变换,仿射变换属于透视变换的特例。透视变换能够保持“直线性”,即原图中的直线,在经透视变换后仍为直线。
透视变换示意图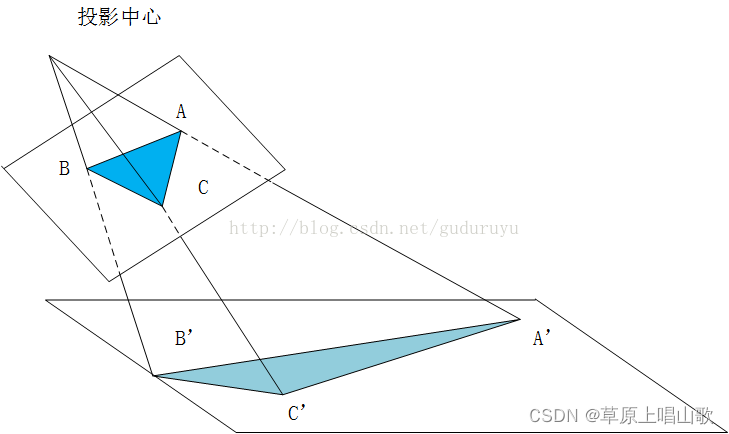
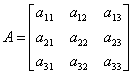
透视变换矩阵变换公式为:

其中透视变换矩阵为:
要移动的点,即源目标点:
定点,即移动到的目标点:
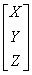
从二维空间变换到三维空间,因为图像在二维平面,故除以Z,(X‘,Y’,Z‘)表示图像上的点。
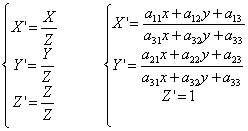
另a33=1,展开上面的公式,可得到一个点为: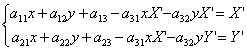
四个点,即可得到8个方程,便可求解出透视变换矩阵A。
透视变换代码:
变换结果
原图
透视变换后的效果图
