openGL系列文章目录
前言
Bui Tuong Phong 在犹他大学的研究生期间开发了一种平滑的着色算法,在1973 年的论文[PH73]中对其进行了描述,并在[PH75]中发表。该算法的结构类似于Gouraud 着色的算法,其不同之处在于光照计算是按像素而非顶点完成。由于光照计算需要法向量N 和光向量L,但在模型中仅顶点包含这些信息,因此Phong 着色通常使用巧妙的“技巧”来实现,其中N和L 在顶点着色器中进行计算,并在光栅化期间插值。图1概述了此策略。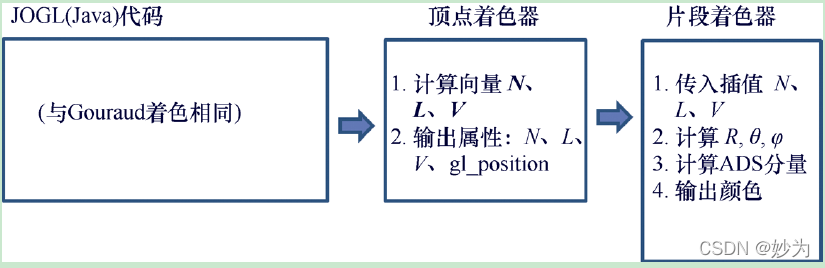
图1
C++/OpenGL 代码完全如前。之前部分在顶点着色器中完成的过程现在回放入片段着色器中进行。法向量插值的效果如图2 所示。现在我们已经准备好使用Phong 着色实现位置光照射下的环面了。大多数代码与实现Gouraud 着色的代码相同。由于C++/OpenGL 代码完全没有改变,在此我们只展示修改过的顶点着色器和片段着色器,如图3所示,Phong 着色修正了Gouraud 着色中出现的伪影。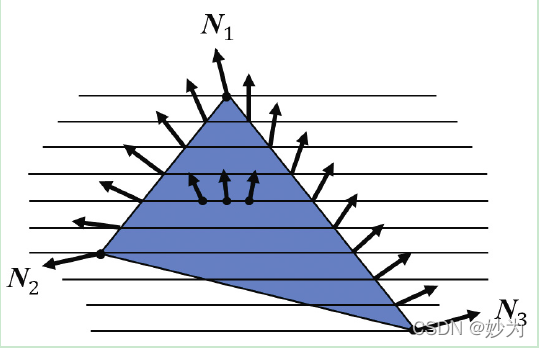
图2
图3
顶点着色器
片元着色器
虽然Phong 着色有着比Gouraud 着色更真实的效果,但这是建立在增大性能消耗的基础上的。James Blinn 在1977 年提出了一种对于Phong 着色的优化方法[BL77],被称为Blinn-Phong反射模型。这种优化是基于观察到Phong 着色中消耗最大的计算之一是解出反射向量R。Blinn 发现向量R 在计算过程中并不是必需的——R 只是用来计算角φ 的手段。角φ 的计算可以不用向量R,而通过L 与V 的角平分线向量H 得到。如图4 所示,H 和N 之间的角α 刚好等于1⁄2(φ)。虽然α 与φ 不同,但Blinn 展示了使用α 代替φ 就已经可以获得足够好的结果。角平分线向量可以简单地使用L+V 得到(见图5),之后cos(α)可以通过•) )H N的点积计算。
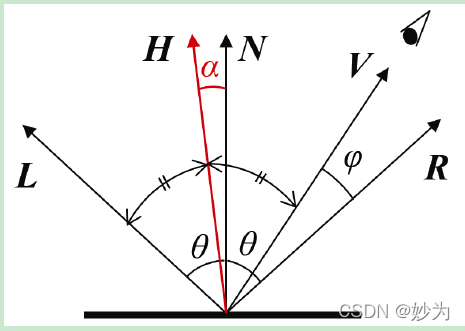
图4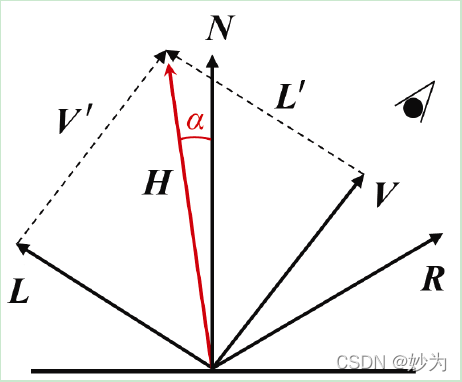
图5
这些计算可以在片段着色器中进行,甚至为了性能考虑(经过一些调整)也可以在顶点着色器中进行。图6 展示了使用Blinn-Phong 着色的环面。它在图形质量上几乎与Phong渲染相同,同时节省了大量性能损耗。
图6
程序3 中展示了修改后顶点着色器和片段着色器,它们用来将程序7.2 中的Phong 着色示例转换为Blinn-Phong 着色。C++ / OpenGL 代码与之前一样没有变化。
程序3 Blinn-Phong 着色的环面
顶点着色器
片元着色器

图7
参考
计算机图形学编程 使用OpenGL和C++
