变换器结构: 定位编码( 参考)
文章目录
- 题目
- 地方(地方)的污染(地方)
- 简介
- 顺序的重要性
- 变形者把它带进来的目的是什么?
- 它是什么
- 怎么实现
- 变换码编码位置
- 相对性证明
题目
地方(地方)的污染(地方)
简介
顺序的重要性
缺乏秩序的声明是缺乏精神的。好像一个人的前言没有加起来你完全疯了语言是人类交流的方式。这是个人交流最直接、最快速的方法之一因此,为了让人们理解你所说的话,必须按工作顺序进行。
变形者把它带进来的目的是什么?
它在Q、K和V矩阵之间的变异器中确定。这是每个单词的一次性计算。这不像RNN没有 一系列的关系 每时每刻。这似乎在某种程度上限制了变形器的进化。以下哪些句子缺乏顺序?所以,必须执行位置编码!
它是什么
我们读到这个时,我们有一个一般的认识,即定位代码对于弥补原始注意下没有时间序列信息的重要性,因此,句子中的每个字都根据其位置信息被标记为二次处理。
怎么实现
为了解决这一问题,我们必须首先理解为什么我们使用位置代码。 换句话说,原始的矢量一词缺少什么?
时序!
时间顺序是什么? 问题是,好像每一天都用一个独特的数字日期来表示,所以无法想象在同一天有同样的两天,日期和日期之间有相对的关系,例如今天前的昨天和后天。
因此,对地点编码必须具备下列特性:
变换码编码位置
文件中的公式如下:
P
E
(
p
o
s
,
2
i
)
=
s
i
n
(
p
o
s
/
1000
0
2
i
/
d
m
o
d
e
l
)
P
E
(
p
o
s
,
2
i
+
1
)
=
c
o
s
(
p
o
s
/
1000
0
2
i
/
d
m
o
d
e
l
)
P E(pos,2i) = sin(pos/10000^{2i/d_{model}})\ P E(pos,2i+1) = cos(pos/10000^{2i/d_{model}})
P
E
(
p
o
s
,
2
i
)
=
s
i
n
(
p
o
s
/
1
0
0
0
0
2
i
/
d
m
o
d
e
l
)
P
E
(
p
o
s
,
2
i
+
1
)
=
c
o
s
(
p
o
s
/
1
0
0
0
0
2
i
/
d
m
o
d
e
l
)
现在让我们改变方案。
偶数位置
P
E
(
p
o
s
,
2
i
)
=
s
i
n
(
p
o
s
/
1000
0
2
i
/
d
m
o
d
e
l
)
P E(pos,2i) = sin(pos/10000^{2i/d_{model}})
P
E
(
p
o
s
,
2
i
)
=
s
i
n
(
p
o
s
/
1
0
0
0
0
2
i
/
d
m
o
d
e
l
)
p
o
s
pos
p
o
s
它提到句子中这个词的位置。
t
=
p
o
s
t=pos
t
=
p
o
s
,
w
i
=
1
1000
0
2
i
/
d
m
o
d
e
l
w_i= frac{1}{10000^{2i/d_{model}}}
w
i
=
1
0
0
0
0
2
i
/
d
m
o
d
e
l
1
这篇文章是全球之声在线特稿的一部分。
w
w
w
罪的角形频率由上述表达式表示,上述表达式可以写成
P
E
(
t
,
2
i
)
=
s
i
n
(
w
i
t
)
【
表 图表
闪闪
我,我,我,我,我,我,我,我,我,我,我,我,我,
计数
位数位数
另一个组织者(_A)
它.. 它.. 它.. 它.. 它..
增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编
《法典法典法典》
】
(w_it) = PE( t, 2i)
P
E
(
t
,
2
i
)
=
s
i
n
(
w
i
t
)
【
表
示
偶
数
位
置
的
编
码
】
奇数位置
P
E
(
p
o
s
,
2
i
+
1
)
=
c
o
s
(
p
o
s
/
1000
0
2
i
/
d
m
o
d
e
l
)
P E(pos,2i+1) = cos(pos/10000^{2i/d_{model}})
P
E
(
p
o
s
,
2
i
+
1
)
=
c
o
s
(
p
o
s
/
1
0
0
0
0
2
i
/
d
m
o
d
e
l
)
同理。
p
o
s
pos
p
o
s
它提到句子中这个词的位置。
t
=
p
o
s
t=pos
t
=
p
o
s
,
w
i
=
1
1000
0
2
i
/
d
m
o
d
e
l
w_i= frac{1}{10000^{2i/d_{model}}}
w
i
=
1
0
0
0
0
2
i
/
d
m
o
d
e
l
1
这篇文章是全球之声在线特稿的一部分。
w
w
w
COs 角频率由上述表达式表示,而以上表达式可以是书面表达式
P
E
(
t
,
2
i
+
1
)
=
c
o
s
(
w
i
t
)
【
表 图表
闪闪
琪琪.. 琪琪.. 琪琪.. 琪琪.. 琪琪..
计数
位数位数
另一个组织者(_A)
它.. 它.. 它.. 它.. 它..
增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编 增编
《法典法典法典》
】
cos(w_it) = PE( t, 2i+1) = PE( t, 2i+1)。
P
E
(
t
,
2
i
+
1
)
=
c
o
s
(
w
i
t
)
【
表
示
奇
数
位
置
的
编
码
】
这些可以放在一个公式中。
P
E
(
t
,
j
)
=
{
s
i
n
(
w
i
t
)
j
=
2
i
c
o
s
(
w
i
t
)
j
=
2
i
+
1
PE(t,j) = begin{cases} sin(w_it) j=2i\ cos(w_it) j=2i+1 end{cases}
P
E
(
t
,
j
)
=
{
s
i
n
(
w
i
t
)
j
=
2
i
c
o
s
(
w
i
t
)
j
=
2
i
+
1
以下是如何使用 j 来编码位置的解释。而不是仍旧使用i,这是因为单方用奇异的娃娃表示。我一开始是[0,1,2.. ]奇数代码从[1,3,5] 不等,甚至数字也从[0, 2, 4..]编码,而奇数则从[0, 2, 4..]编码。密码是词的位置代码
但是,当两者合并时,需要一个新的数字来合并这两个数字,以便它们可以继续从零开始,而变化是j。
根据公式理解的过程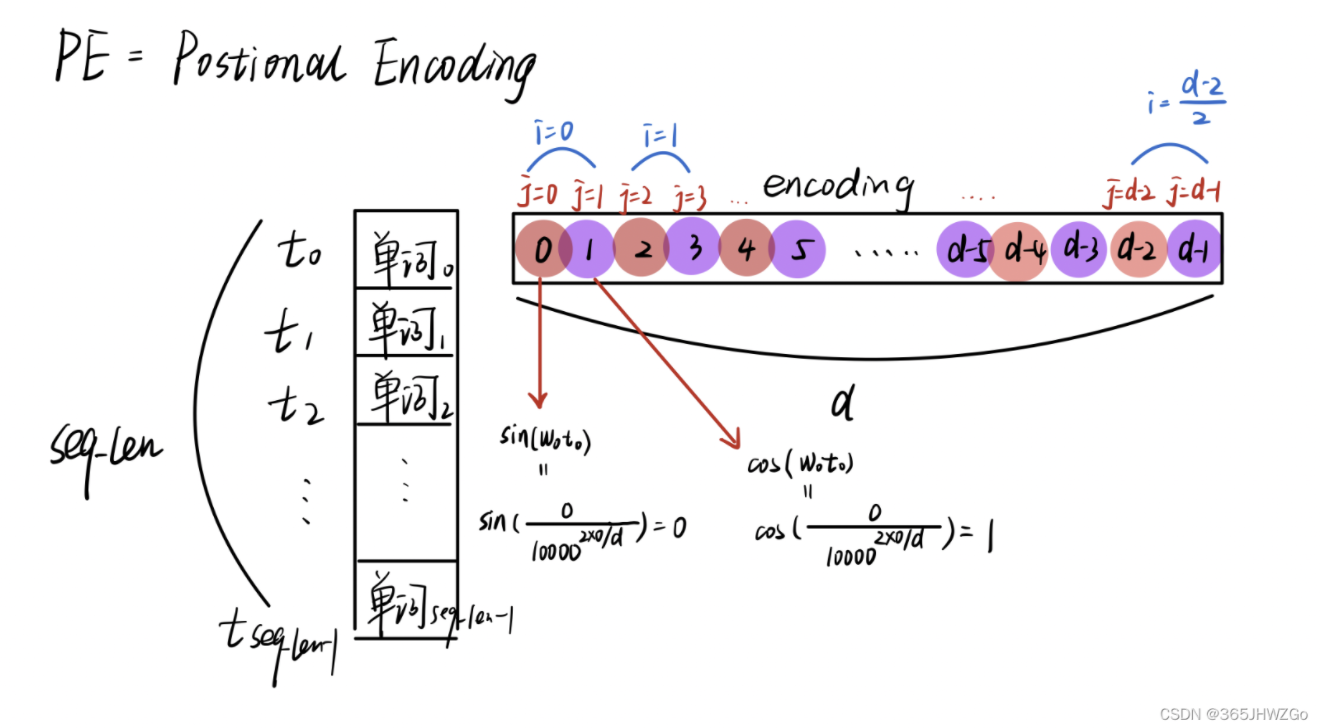
w
i
=
1
1000
0
2
i
/
d
m
o
d
e
l
w_i= frac{1}{10000^{2i/d_{model}}}
w
i
=
1
0
0
0
0
2
i
/
d
m
o
d
e
l
1
你可以注意到它如何变小 当我变大。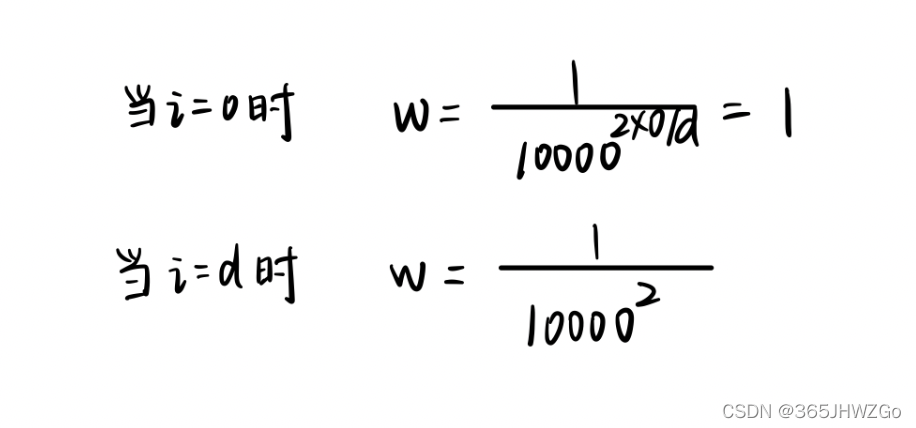
使用图表显示编码进程 。
使用 imshow 显示显示
每个单词现在都指定一个位置代码。
结果发现嵌入代码之后的维度是..
d
w
o
r
d
e
m
b
e
d
d
i
n
g
d_{word embedding}
d
w
o
r
d
e
m
b
e
d
d
i
n
g
未来可确保将其添加到最初的维度中,因此确保位置的维度编码d=
d
w
o
r
d
e
m
b
e
d
d
i
n
g
d_{word embedding}
d
w
o
r
d
e
m
b
e
d
d
i
n
g
,即
d
w
o
r
d
e
m
b
e
d
d
i
n
g
=
d
p
o
s
i
t
i
o
n
a
l
e
m
b
e
d
d
i
n
g
d_{word embedding}=d_{positional embedding}
d
w
o
r
d
e
m
b
e
d
d
i
n
g
=
d
p
o
s
i
t
i
o
n
a
l
e
m
b
e
d
d
i
n
g
相对性证明
我们现在有了位置代码,它可以很容易地用于文字嵌入,通过输入文字序列来改进模型输入。
那么,它如何编码 这个词的相对位置?
下面是我们要展示的!
先举一个例子:
假设声明是"我明天要吃东西"
| 我 | 明天 | 要 | 吃饭 |
|---|---|---|---|
| t 0 t_0 t 0 | t 1 t_1 t 1 | t 2 t_2 t 2 | t 3 t_3 t 3 |
如果位置代码正确,我应该能够接收 明天我搬到右侧的单位之一。
即证明
P
E
(
t
+
k
,
j
)
=
M
∗
P
E
(
t
,
j
)
PE(t+k,j)=M*PE(t,j)
P
E
(
t
+
k
,
j
)
=
M
∗
P
E
(
t
,
j
)
,
M
M
M
为一个矩阵,
P
E
(
t
,
j
)
PE(t,j)
P
E
(
t
,
j
)
可通过线性修改获得。
P
E
(
t
+
k
,
j
)
PE(t+k,j)
P
E
(
t
+
k
,
j
)
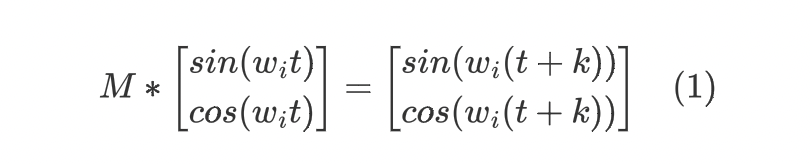
证明
(1)式可以简写成
M
∗
A
=
B
(
2
)
M*A=B (2)
M
∗
A
=
B
(
2
)
因为A的维度为
(
2
,
1
)
(2,1)
(
2
,
1
)
,B的维度为
(
2
,
1
)
(2,1)
(
2
,
1
)
,所以M的维度为
(
2
,
2
)
(2,2)
(
2
,
2
)
这就是你如何获得第三。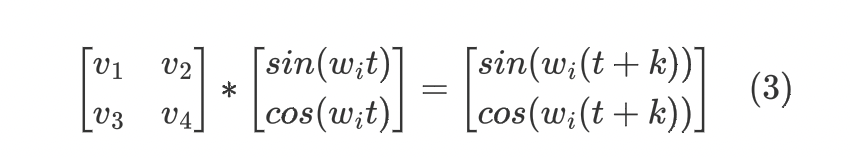
由(3)式展开为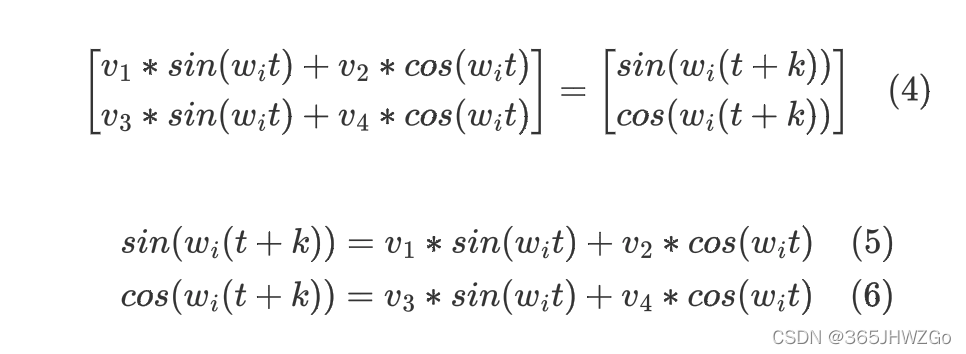
根据三角公式
s
i
n
(
A
+
B
)
=
s
i
n
A
c
o
s
B
+
c
o
s
A
s
i
n
B
c
o
s
(
A
+
B
)
=
c
o
s
A
c
o
s
B
−
s
i
n
A
s
i
n
B
sin(A+B)=sinAcosB+cosAsinB\ cos(A+B)=cosAcosB-sinAsinB
s
i
n
(
A
+
B
)
=
s
i
n
A
c
o
s
B
+
c
o
s
A
s
i
n
B
c
o
s
(
A
+
B
)
=
c
o
s
A
c
o
s
B
−
s
i
n
A
s
i
n
B
(5)和(6)扩大,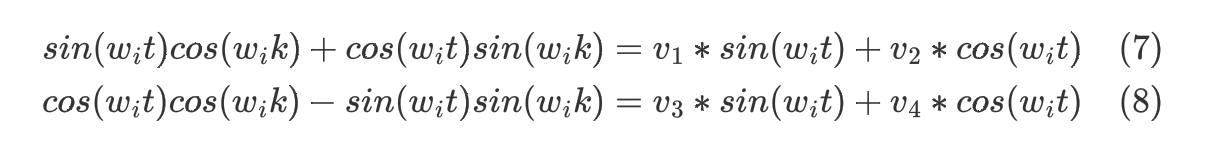
根据等式得
M
=
[
v
1
v
2
v
3
v
4
]
=
[
c
o
s
(
w
i
k
)
s
i
n
(
w
i
k
)
−
s
i
n
(
w
i
k
)
c
o
s
(
w
i
k
)
]
M=left[ begin{matrix} v_1 & v_2 \ v_3&v_4\ end{matrix} right]=left[ begin{matrix} cos(w_ik) & sin(w_ik) \ -sin(w_ik)&cos(w_ik)\ end{matrix} right]
M
=
[
v
1
v
3
v
2
v
4
]
=
[
c
o
s
(
w
i
k
)
−
s
i
n
(
w
i
k
)
s
i
n
(
w
i
k
)
c
o
s
(
w
i
k
)
]
M
M
M
是一个和
t
t
t
重要的不是矩阵 而是偏转
w
i
w_i
w
i
和偏移量
k
k
k
有关
如下图所示这个过程
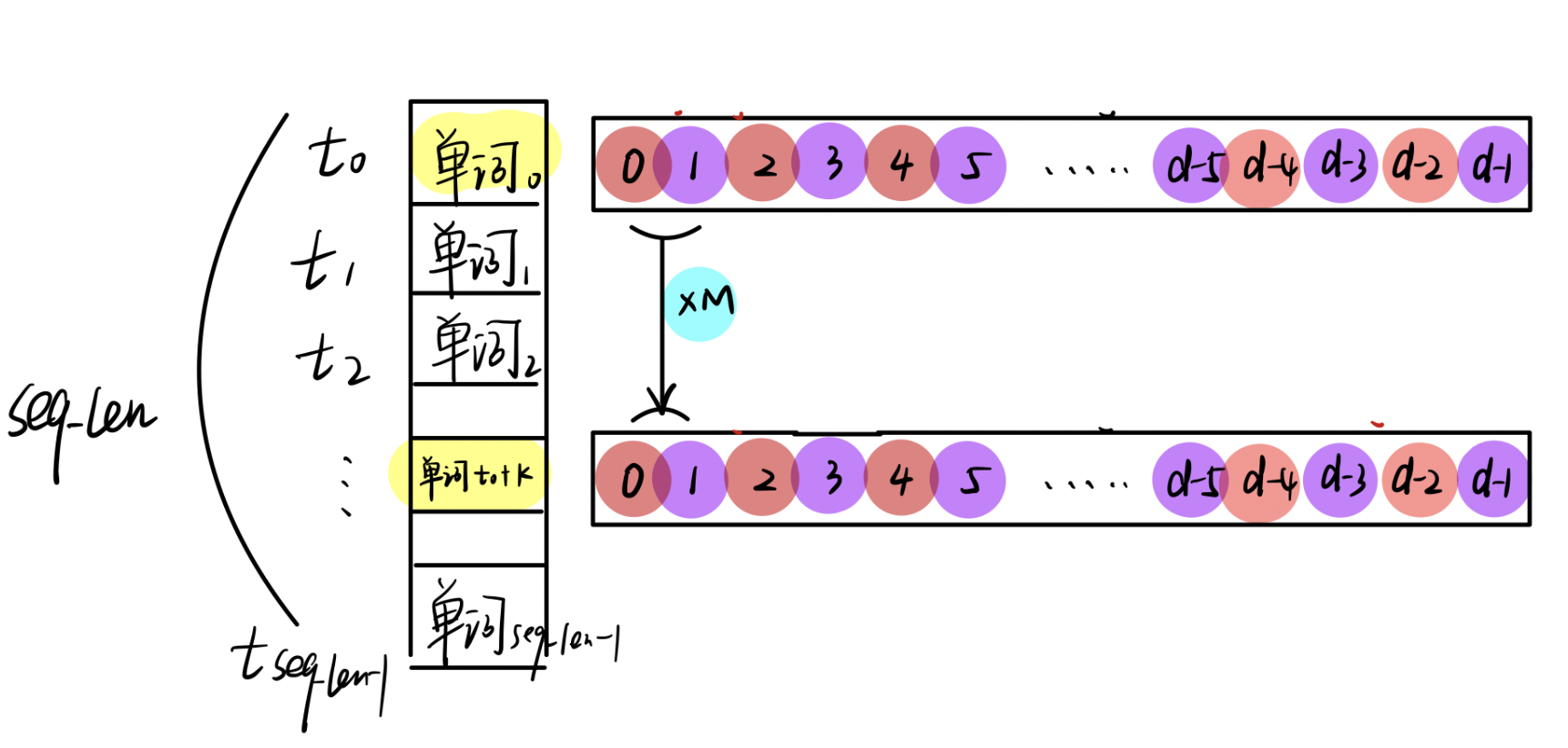
任何单词都可以通过线性矩阵流动这一事实反映了其相对性。 M M M 改变之后再换个词
这是一个极好的网站 用于原始应用机制 同时处理文字矢量, 所以位置代码已经过时了。
